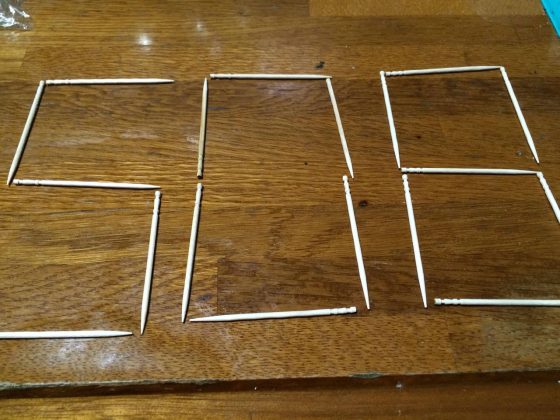『0』の1行目の横向きつまようじと3行目の横向きのつまようじを取り出すと『0』が『11』に変わります。
ここまではさっきと同じなのですが、取り出した2本のつまようじを
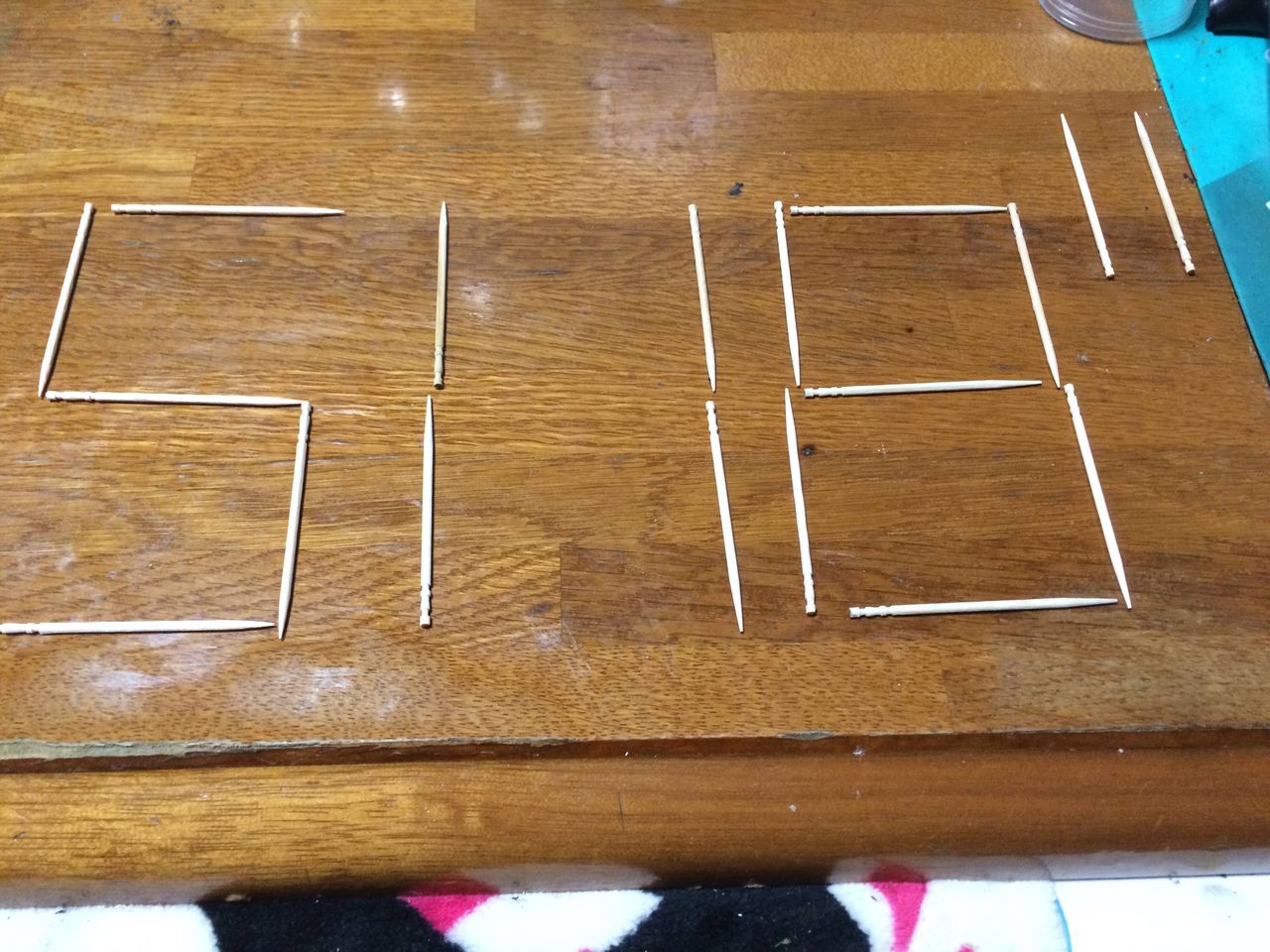
指数として使うと『5118の11乗]』となります。
5118×5118×5118×5118×5118×5118×5118×5118×5118×5118×5118の答えなので正にけた違いです。
ただ『5118』を180°ひっくり返してみると『8115』なので
『8115の11乗』の方が最大ですね。
さらに数字の表記の大きさを無視すると

11の5118乗や、11の8115乗が作れるので、こちらの方がさらにさらに桁違いに大きな数となりますが、
まあこれは数字の表記の大きさでちょっとインチキをしているので、
答えは『8115の11乗』となります。
自分の導き出した答えが
①3桁で最大を探した方は、問題をそのまま捉えてしまった方
②4桁~5桁の数を思いついた方は、デジタル数字の表記内で創意工夫した方
③そして、指数表記に気づいた方は(上の答え以外でもOK(例)505の11乗))、そうとう柔軟な発想力を持った方
となります。
ボクのなかでは、数学の図形の超応用問題(山口県の公立入試で置き換えると、図形の証明に出てくる計算問題)に
通じる考え方とも言えなくもないかなぁって感じでした。